CBSE Class 9 board Lab Manual activity : a^2 – b^2 = (a-b)(a+b)

By
-
0
453

algebraic identity : a2 + b2 = (a-b)(a+b)

ALGEBRAIC IDENTITIES : The algebraic equations which hold true for all values of variables assigned to them are known as algebraic identities. They are used for the factorization of algebraic polynomials. In this way, algebraic identities are used in the formulation of algebraic polynomials and solving them. In this article, we will consider and explain one such algebraic identity : a2 + b2 = (a-b)(a+b) , which is majorly used in MIDDLE-TERM Splitting method for solving equations, by using paper cutting and pasting activity along with examples.

This algeraic identity helps in solving the algebraic polynomials by factorization.

Suppose we have to find the product of 98 and 102, we will use identity : a2 – b2 = (a-b)(a+b) as follows –

we will simply factorize them using 98=100-2 and 102=100+2 ,

98 x 102

= (100-2) (100+2) [form : (a-b)(a+b) where a=100 and b=2 ]

= 1002 – 22 [using : (a-b)(a+b) = a2 – b2 ]

= 10000 – 4

= 9996 .

LAB MANUAL ACTIVITY :

AIM

To prove : a2 + b2 = (a-b)(a+b) practically using paper.

Formulas used

  1. Area of square = a x a = a2 (a = Side of square)
  2. Area of rectangle = l x b = lb (l = length of rectangle and b = breadth of rectangle)

Materials needed

  1. Plain sheet (white)
  2. 2 different Glazed / colored paper (here, green and red)
  3. A pair of scissors
  4. glue

Procedure / Steps to follow

>> Take any 2 different numbers for a and b such that a > b. Let’s take a = 5 and b = 4 (5 > 4 i.e, a>b ).

Steps :

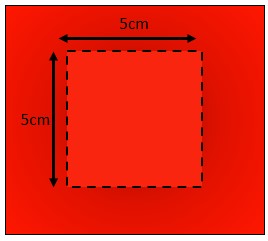
STEP 1 – Draw square of 5 cm on red paper.

figure – 1

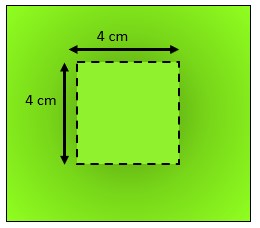
STEP 2 – Draw square of 4 cm on green paper.

figure – 2

STEP 3 – CUT out these squares. PASTE them on a plain white sheet. LABEL them as given in below.

figure – 3

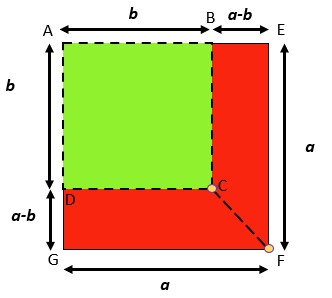
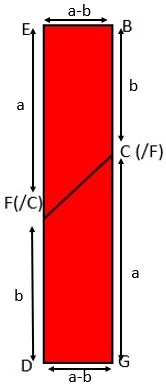
STEP 4 – Cut the red portion along CF and dotted lines. We get 2 quadrilaterals as BEFC and DGFC. This part identifies with a2-b2

figure – 4

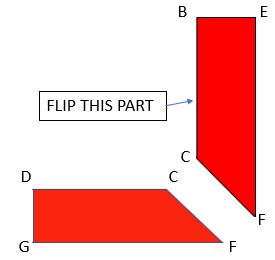
STEP 5 – Place these two quadrilaterals on other white sheet of paper such that we get a rectangle of area = (a-b)(a+b).

figure – 5

CALCULATIONS and OBSERVATION

In figure – 1, Area of square AEFG = a2 = (5)2 = 25 cm2
figure – 2 , Area of square ABCD = b2 = (4)2 = 16 cm2
figure – 3 , Area of quadrilateral BEFC + area of quadrilateral DGFC = area of AEFG – area of square ABCD
= (a2 – b2) cm2
= 25 – 16
= 9 cm2 …(i)
figure – 5 , Area of rectangle EBGD = EB x ED
= (a – b)(a+b)
= (5 – 4)(5 + 4)
= 1 x 9 = 9 cm2 …(ii) From (i) and (ii), a2 + b2 = (a-b)(a+b) .

Read More : A SQUARE MINUS B SQUARE ( A2 – B2 ) – Study Equation

RELATED ARTICLESMORE FROM AUTHOR