
The A SQUARE MINUS B SQUARE ( a2 – b2 ) formula is used to get the difference between two or many squares in an equation. The (a+b)(a-b) formula can be used to obtain the a2 – b2 formula quickly. In the following parts, let’s study them with a few cases that have been solved. The a2 – b2 formula is also recognized as the “difference of squares formula.” A square SUBTRACTED b square is used to compute the squares’ disparity rather than just calculating the squares themselves. The mathematical algebraic equation (a+b) (a-b) has been proven using two distinct methods.
Formula:
a2 – b2 =(a – b) (a + b)
Algebraic Approach
The algebraic expression a2 – b2 denotes the distinction between the two square integers. It may be seen as combining two exceptional binomials, a+b and a-b. Mathematical factorization allows for determining the differential of squares’ factoring value using algebraic equations.
Method 1:
Let’s examine the a square minus b square formula’s proof. In order to demonstrate that LHS = RHS, we must establish that a2 – b2 = (a – b) (a + b). Let’s attempt to figure out the equation:
a square – b square equals (a – b) + (a + b)
The result of multiplying (a – b) and (a + b) is =a(a+b).
In other words, -b(a + b) = a2 + ab – ba – b2 = a2 + 0 + b2 = a2 – b2
As a result, Verified a2 – b2 = (a – b) (a +b).
Geometric Approach:
The a2-b2 identity may be expressed as a scaled product of the binomials a+b and a-b to show the differences between the two fair values. The areas of geometric patterns can be used to determine the factoring form of the a2-b2 equation mathematically.
square-area subtraction:
1. Assume a square with sides, each being one unit long. Consequently, a2 is the square’s area.
2. At each corner of the small square, make a small square with both a side of b units. Therefore, b2 is the little square’s area.
3. The square having area b2 should then be subtracted from the court with area a2. It establishes a different geometric form whose area equals a2 – b2.
Divide the Modified Shape’s Area
Start dividing the newly reduced geometric form into two separate rectangles, with one of the rectangles’ lengths similar to one unit.
Regarding the upper rectangle: This rectangle has a breadth of and a length of in geometry units.
Identically study the lower rectangle. This rectangle has a width equal to units and a length of units.
Square Distinction through Factoring Method
Dimensionally, the length of the bottom rectangle is also a-b, as is the width of the top rectangle, which is a – b. The widths of both rectangles match if the bottom rectangle is turned to 90 degrees, making it helpful to combine them into a single rectangle.
Split the two rectangles.
Merge the two rectangles after turning the lower rectangle 90 degrees. Another rectangle was created.
The resulting rectangle’s length and width are multiplied by b and divided by a. As a result, (a+b)(a-b) is the area of this rectangle.
In the first phase, it is shown that the area of a subtracted shape is equal to a square minus a square of b, and this same shape is now turned into a rectangle whose area is similar to (a + b) (a – b ).
As a result, mathematically speaking, the areas of both forms ought to be equal. Therefore :
a^2 – b^2 = (a+b)(a- b)
In geometry, it is established that the product of the binomials (a+ b) and (a – b) equals the square subtracted from the b square.
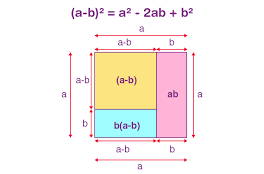
Evidence for the a2–b2 equation:
The argument for why (a + b) equals the value of a2 – b2 (a – b). Let’s think about the image above. Consider the two squares with sides a and b, respectively. This may be shown as the product of the areas of two rectangles. On one side of a rectangle is a length of one unit and a width of (a – b) units. On the other side, there is a length of (a – b) and a width of b units. To get the consequent values, sum the areas of the two rectangles. The two rectangles’ respective areas are (a – b) a = a(a – b) and (a – b) b = b. (a – b). The actual produced resulting expression, i.e., a(a + b) + b(a – b) = (a + b), is the sum of the areas of rectangles (a – b). The result of one more rearrangement of the various squares and rectangles is (a+b)(ab)=a2b2.
Explain Steps on Using the a2 – b2 Formula.
When applying the a2 – b2 formula, the steps below are taken.
1. First, look at the pattern of the numerals to see if they have a power of 2 or not.
2.The equation for a2 – b2 is written as a2 – b2 = (a – b) (a + b).
3. Simplify the a2 – b2 formula by replacing the values of a and b.
Examples of the formula a2-b2
A SQUARE MINUS B SQUARE ( a2 – b2 ) Question and Answers
Using the a2-b2 formula, determine the result of 1062 – 62.
Solution: The area to search for is 1002 – 62.
Assume that an is 100 and b is 6.
We will substitute them in the a2 – b2 calculation instead.
(a – b) (a + b) = a2 – b2
1062 – 62 = (106 + 6) (106 – 6)
= (100) (112)
= 11200
Factorize the formula 25×2 – 64.
Solution: 25×2 – 64 has to be factored in.
To factorize this, users shall apply the a2 – b2 formula.
The above expression can be written as
25×2 – 64 = (5x)2 – 82
In the formula for a2 – b2, we will substitute a = 5x and b = 8 instead.
(a – b) (a + b) = a2 – b2
(5x)2 – 82 = (5x + 8)(5x – 8)
Apply the a2 – b2 formula to reduce 102 – 52.
The answer is to find 102 – 52.
Suppose that a is ten and b are 5.
Applying the equation (a – b) = (a – b) (a + b)
102-52 = (10 – 5) (10 + 5) Equals 10(10 +5) – 5(10 + 5) = 10(15) – 5(15) \s= 150-75 = 75
102 minus 52 equals 75.
Solve 3a2 – 2b2 as an example.
Solution: It continues as:
Provided equation 3a2 – 2b2 (i.e., a2 – b2) denotes identity third.
If a = 3a and b = 2b, then
Applying the values of the parameters a and b to the identity, i.e., a2 – b2 = (a + b) (a – b), we obtain:
3a2 – 2b2 = (3a + 2b) (3a – 2b)
Consequently, 3a2 – 2b2 = 3a + 2b (3a – 2b)
Solve (6m + 9n) in Example 2. (6m – 9n)
Solution: This continues as:
The provided equation (6m + 9n) (6m – 9n) denotes the identity third, or a2 – b2.
a = 6 m, whereas b = 9 n
Applying the values of the variables a and b to the equation, i.e., a2 – b2 = (a + b) (a – b), we obtain:
(6m + 9n) (6m – 9n) = (6m)2 – (9n) 2
We obtain = 36m2 – 81n2 by extending the exponential expressions on the LHS.
The result is that (6m + 9n) (6m – 9n) = 36m2 – 81n2.
What Is the Formula of a Square Minus B Square
The formula of a2 – b2 is (a+b)(a-b).
Read More : How To Calculate SGPA From Grade Online – Study Equation